上大学的时候，在C语言课程上就会讲述冒泡排序，这应该是所有编程课里面都会讲到的经典排序之一。冒泡排序的思想很经典，也便于初学者来掌握，从而让广大编程者打开算法的大门。下面我们首先讲一下冒泡排序，讲完冒泡排序，我们会讲一下选择排序，之所以把它们放在一起讨论，是因为它们在排序思想上有所类似，但是又有不同之处。

一、冒泡排序
首先，我们来明确下排序的定义：将一组无序的数，经过代码排序以后，输出由小到大或者由大到小的有序序列。
如无序数组：[2,3,1]
排序后结果为：[1,2,3]

那么，冒泡排序是怎么排序的呢？

(1)冒泡排序思想
记得大学老师跟我们讲冒泡排序的时候，就用了气泡在水中冒出来，气泡越大的水泡越有机会冒得更快更高（这里不是物理哈，只是直观说法）。冒泡算法的说法很形象，就是大的不算往上冒，冒过的泡不再冒，直到这个数组有序。

(2)冒泡步骤
把数组当做一组排队的人，并且编号。那么就有一个队列，编号分别为：2，3，1。

1.让排头的同学（即编号为2）往后面比较，如果自己的编号比后面的同学大，那么两者交换位置，如果不大，则让不交换位置。
2.当步骤一完成后，轮到位置为2的同学（此时编号为3，因为步骤1没有交换）和后一个同学进行比较，如果位置为2的同学比后一个同学的编号大，则两者交换。
3.不管交换与否，都会轮到下一个同学和后面的一个同学进行比较并视情况进行交换，轮到最后一个同学位置。
4.最后记录下已经冒泡成功的位置，下一轮比较序列中不再像该同学比较，直到整个序列完成(即冒泡成功的位置是2)。
那么，按照上面的步骤，无序数组[2，3，1]的排序过程为：

1.位置1的同学和位置2的同学进行比较，发现无法交换，此时序列为：[2,3,1]，下一个交换位置为2。
2.位置2的同学和位置3的同学进行比较，发现可以交换，此时序列为：[2,1,3]，下一个交换位置为3。
3.位置3的同学发现无法继续进行交换，此时序列为：[2,1,3]，记录已成功排序数为位置3，下一次从头开始。
4.位置1的同学和位置2的同学进行比较，发现可以交换，此时序列为：[1,2,3],下一个交换位置为2。
5.位置2的同学试图和位置3比较，但是发现位置3的同学在上一轮已经比较成功，所以此轮比较结束，记录成功位置为2，此时序列为[1,2,3]
6.轮到位置1的同学试图和位置2进行比较，发现位置2已经是成功冒泡的位置，整个排序结束。
从上面可以看出，冒泡排序就是两两比较，两两交换，直到结束。如果对上面的文字看着头晕，那么这里引用一个网友的句子：

举例说明：要排序数组：[6,3,8,2,9,1];

第一趟排序：

　　　　第一次排序：6和3比较，6大于3，交换位置： 3 6 8 2 9 1

　　　　第二次排序：6和8比较，6小于8，不交换位置：3 6 8 2 9 1

　　　　第三次排序：8和2比较，8大于2，交换位置： 3 6 2 8 9 1

　　　　第四次排序：8和9比较，8小于9，不交换位置：3 6 2 8 9 1

　　　　第五次排序：9和1比较：9大于1，交换位置： 3 6 2 8 1 9

　　　　第一趟总共进行了5次比较， 排序结果： 3 6 2 8 1 9

第二趟排序：

　　　　第一次排序：3和6比较，3小于6，不交换位置：3 6 2 8 1 9

　　　　第二次排序：6和2比较，6大于2，交换位置： 3 2 6 8 1 9

　　　　第三次排序：6和8比较，6大于8，不交换位置：3 2 6 8 1 9

　　　　第四次排序：8和1比较，8大于1，交换位置： 3 2 6 1 8 9

　　　　第二趟总共进行了4次比较， 排序结果： 3 2 6 1 8 9

第三趟排序：

　　　　第一次排序：3和2比较，3大于2，交换位置： 2 3 6 1 8 9

　　　　第二次排序：3和6比较，3小于6，不交换位置：2 3 6 1 8 9

　　　　第三次排序：6和1比较，6大于1，交换位置： 2 3 1 6 8 9

　　　　第二趟总共进行了3次比较， 排序结果： 2 3 1 6 8 9

第四趟排序：

　　　　第一次排序：2和3比较，2小于3，不交换位置：2 3 1 6 8 9

　　　　第二次排序：3和1比较，3大于1，交换位置： 2 1 3 6 8 9

　　　　第二趟总共进行了2次比较， 排序结果：2 1 3 6 8 9

第五趟排序：

　　　　第一次排序：2和1比较，2大于1，交换位置： 1 2 3 6 8 9

　　　　第二趟总共进行了1次比较， 排序结果： 1 2 3 6 8 9

最终结果：1 2 3 6 8 9

总结起来，我们用一句话来描述：N个数字要排序完成，总共进行N-1趟排序，每i趟的排序次数为(N-i)次，所以可以用双重循环语句，外层控制循环多少趟，内层控制每一趟的循环次数。
(3)代码实现
其java实现代码为：

for(int i=1;i<arr.length;i++){ // 数据序列的长度，要排n个数

    for(int j=1;j<arr.length-i;j++){ //每一次要减掉已经完成冒泡的个数

        //switch the num
        if(arr[j]>arr[j+1]){ //如果比后一个大，则交换 
　　　　　　int temp=arr[j];
　　　　　　arr[j]=arr[j+1];
　　　　　  arr[j+1]=temp;
　　　　}
    }
} 

至此，我们已经完成冒泡算法。

二、冒泡排序复杂度
冒泡排序的优点：

每进行一趟排序，就会少比较一次，因为每进行一趟排序都会找出一个较大值。如上例：第一趟比较之后，排在最后的一个数一定是最大的一个数，第二趟排序的时候，只需要比较除了最后一个数以外的其他的数，同样也能找出一个最大的数排在参与第二趟比较的数后面，第三趟比较的时候，只需要比较除了最后两个数以外的其他的数，以此类推……也就是说，没进行一趟比较，每一趟少比较一次，一定程度上减少了算法的量。

用时间复杂度来说：

　　1.如果我们的数据正序，只需要走一趟即可完成排序。所需的比较次数C和记录移动次数M均达到最小值，即：Cmin=n-1;Mmin=0;所以，冒泡排序最好的时间复杂度为O(n)。

　　2.如果很不幸我们的数据是反序的，则需要进行n-1趟排序。每趟排序要进行n-i次比较(1≤i≤n-1)，且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下，比较和移动次数均达到最大值：

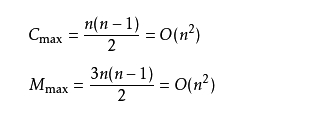
冒泡排序的最坏时间复杂度为：O(n2) 。

综上所述：冒泡排序总的平均时间复杂度为：O(n2) 。

不过值得注意的是，在n很小的时候，我们尽可以放心使用冒泡排序，简单易用。

标签: 算法基础, 选择排序, 冒泡排序